What is the point of Cauchy-Schwarz, Minkowski and Hölder inequalities?

These three inequalities often tend to appear as a package in many textbooks about real analysis, signal processing or linear algebra. It is good to know the main reason that we see this package all the time, and to separate the role of each of these three fundamental inequalities.

The overall reason is that, these inequalities are the key to generalize the facts about vectors in 2D/3D spaces and the Euclidean norm to higher dimensional spaces and (non-Euclidean) $p$-norms. Each of these inequalities will have very specific roles in this regard, and without delving into details or proving them, we’ll just try to highlight this main role.

Cauchy-Bunyakoovsky-Schwarz (a.k.a. Cauch-Schwarz)

We’ve written about this inequality in more detail here, but here we’ll summarize again its role within this 3-pack of inequalities.

A norm is a function $||\cdot||$ of a vector that satisfies three properties. The property that’s least easy to prove is typically the triangle inequality:
$$
||x+y|| \leq ||x|| + ||y||
$$
And this is precisely where the CBS enters. To remind, CBS dictates that
$$
|x^*y| \leq ||x||_2 ||y||_2
$$
The main role of this inequality is to show that the triangle inequality of the Euclidean norm $||\cdot||_2$ is valid not only for 2D or 3D spaces, but also for higher dimensional spaces. Here is a figure showing this role of CBS to carve it in our minds:

Thus, the first role of CBS is to show that the Euclidean norm ($\ell_2$) is valid in high-dimensional spaces. The second role of the CBS is to show that we can talk about angles in higher dimensional spaces. This is extremely critical, since if we can talk about angles, we can talk about orthogonality (i.e., the state of the angle being zero) for the $\ell_2$ norm, thus we can enjoy all the advantages of orthogonality in $\ell_2$ spaces. And here is the figure summarizing this path to generalization.

In fact the CBS inequality holds not only for $\ell_2$ spaces, but any inner product space (e.g., a space of matrices equipped with the $trace()$ norm). The generalized CBS inequality is the key to reach this generalization

In sum, the (general) CBS inequality is the key for showing that:

• The $\ell_2$ norm is a valid norm in high-dimensional spaces
• We can talk about angles between two vectors in high-dimensional $\ell_2$ spaces
• We can talk about orthogonality in high-dimensional $\ell_2$ spaces
• We can talk about orthogonality in any space equipped with a norm generated from an inner product

Hölder’s and Minkowski’s Inequalities

Hölder’s inequality is another generalization of the CBS inequality that has different implications. Overall, this inequality is concerned with $\ell_p$ norms for $p\neq 2$ (when $p=2$ it simply reduces to CBS).

Hölder’s inequality shows that for any $p$ and $q$ such that $1/p+1/q=1$ and the corresponding $p$ and $q$ norms $||\cdot||_p$ and $||\cdot||_q$, we have
$$
|x^* y| \leq ||x||_p ||y||_q
$$

As far as our summary is concerned, the main role Hölder’s inequality is to prove the Minkowski inequality:
$$
\left( \sum_{k=1}^{\infty} |x_k+y_k|^{p} \right)^{1/p} \le \left( \sum_{k=1}^\infty |x_k|^p\right)^{1/p}+\left( \sum_{k=1}^\infty |y_k|^p\right)^{1/p}
$$
for any $p \in [1,\infty)$. As you can see, the Minkowski inequality is nothing but the triangle inequality for $\ell_p$ norms! Thus, these inequalities together become the key to prove that $\ell_p$ norms are valid norms in high-dimensional spaces. Here is the corresponding picture to keep in mind:

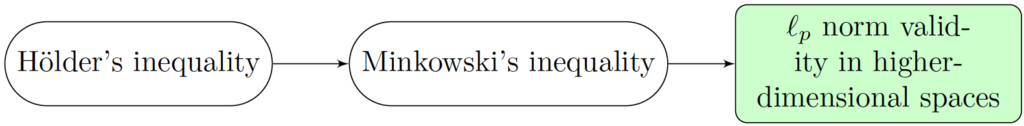
Conclusions

We hopefully now see precisely why these three inequalities are so fundamental for real analysis, and what is the role of each of these. The best summary is just looking at the pictures above. But there is no harm in summarizing again:

• The (general) CBS inequality shows that
  • the Euclidean norm is valid in $\mathbb C^n$ for any positive integer $n$
  • we can talk about orthogonality in any inner-product space
• The Hölder and Minkowski inequalities show that all the $p$-norms are valid norms in $\mathbb C^n$ for any positive integer $n$