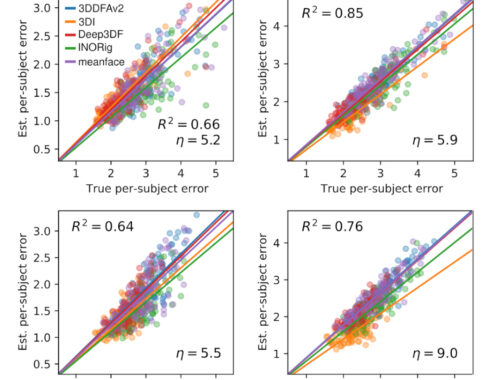
How to prove SVD ? A recipe approach
To prove the existence of SVD is no trivial task, but it turns out that it’s not too difficult either. Looks like one needs a few ingredients (hence the title), but once we know them and understand the overall idea, the proof is not too difficult. Below we list the basic ingredients needed to prove the existence of SVD.
- The URV decomposition $\mathbf{A} = \mathbf{URV} = \mathbf{U}\begin{pmatrix}\mathbf C & \mathbf 0 \\ \mathbf 0 & \mathbf 0\end{pmatrix}\mathbf{V}$
- $||\mathbf{A}||_2 = ||\mathbf{URV}||_2 = \left|\left|\mathbf{U}\begin{pmatrix}\mathbf C & 0 \\ \mathbf 0 & \mathbf 0\end{pmatrix}\mathbf{V}\right|\right|_2 = ||\mathbf{R}||_2$
- $\left|\left|\begin{pmatrix}\mathbf A & 0 \\ 0 &\mathbf{B}\end{pmatrix}\right|\right| = \max\{||\mathbf A||_2, ||\mathbf{B}||_2\}$
- $(\mathbf C^T\mathbf C – \lambda \mathbf I) \mathbf x = \mathbf 0$ for eigenpair $\lambda, \mathbf x$
- Reflectors are orthogonal matrices such that $\mathbf R^T = \mathbf R$
- For any $\mathbf x$, there exists reflector $\mathbf R$ such that $\mathbf{Rx=x}$
- For any $\mathbf x$, there exists reflector $\mathbf R$ such that $\mathbf{R} = \begin{pmatrix}\mathbf x \dots \end{pmatrix}$
- If $\mathbf Q$ is orthogonal, so are $\begin{pmatrix} \mathbf Q & \mathbf 0 \\ \mathbf 0 & \mathbf I\end{pmatrix}$ and $\begin{pmatrix} \mathbf I & \mathbf 0 \\ \mathbf 0 & \mathbf Q\end{pmatrix}$.
In sum, we need to have well comprehended the matrix 2-norm, the existence of URV decomposition (and, possibly, the fundamental theorem of linear algebra), and the concept of reflectors (at least within the scope of the proof provided by C. D. Meyer).
Instead of writing the full proof that I found (p411 of C. D. Meyer), I’ll just try to sketch out the overall idea about how to prove SVD.
Below is the sketch of how the proof proceeds. As it can be seen, the URV gives us a jumpstart: It starts with a decomposition that’s similar to SVD, but the matrix in the middle is not diagonal. We’ll see how we can diagonalize it, without harming the orthonormality of $\mathbf U$ and $\mathbf V$, in the process.
A key property of SVD is that, it not only provides a decomposition with a diagonal matrix in the middle and orthogonal matrices in the sides, but also, the entries on the diagonal of the matrix are the eigenvalues of $\mathbf A^T \mathbf A$ in a decreasing order. Thus, the top-left entry in the diagonal matrix is the largest eigenvalue of $\mathbf A^T \mathbf A$, or, in other words, $||\mathbf A||_2$.
Using our first two ingredients, we can write $||\mathbf A||_2=||\mathbf C||_2$. It is known that the matrix 2-norm is the largest $\lambda$ such that $\mathbf C^T\mathbf C – \lambda \mathbf I$ is singular. Also, by definition of the 2-norm, the $||\mathbf C||_2=\max_{\mathbf x \neq 0} \frac{||\mathbf{Cx}||_2}{||\mathbf{x}||_2}$. Let $\mathbf x$ be the $\mathbf x$ that maximizes $\frac{||\mathbf{Cx}||_2}{||\mathbf{x}||_2}$. Then, $$(\mathbf C^T\mathbf C – \lambda \mathbf I) \mathbf x = \mathbf 0.$$
Now it’s time to use the magic of reflectors. As the figure above suggests, we’ll find reflectors $\mathbf R_x$ and $\mathbf R_y$, such that the first row and column of $$\mathbf R_y\mathbf C\mathbf R_x$$ are zero vectors except their first entry, which is $\sigma_1$ — the largest singular value of $\mathbf A$.
To this end, define $\mathbf y$ as $\mathbf{y=Cx/||Cx||}$. One of our ingredients says that, we can build a reflector $\mathbf R_y$ such that the first column of the reflector is the vector $\mathbf y$, $\mathbf R_y = (\mathbf y | \mathbf Y)$. And since reflectors are orthogonal matrices, $\mathbf R_y^T y = \mathbf R_y y$ will simply be $\mathbf e_1$. This means that, $\mathbf{RCx} = ||\mathbf{Cx}||\mathbf e_1 = \sigma_1\mathbf e_1$. As you may suspect, this is a big step — we took a vector, multiplied it with a matrix such that the first entry of the output is the top-left entry of the diagonal of the SVD (i.e., $\sigma_1$), and the rest is zero. We’ll see that the right-multiplication by $\mathbf R_x$ will do the rest of the job.
And we’ll use a reflector again. Suppose that $\mathbf R_x$ is the reflector whose first column is $\mathbf x$, i.e., $\mathbf R_x = (\mathbf x | \mathbf X)$. Now that we’ve gone through the reflectors, we can evaluate the expression $\mathbf R_y\mathbf C\mathbf R_x$ in more detail: $$ \mathbf R_y\mathbf C\mathbf R_x = \begin{pmatrix} \mathbf y^T \mathbf{Cx} & \mathbf y^T \mathbf{CX} \\ \mathbf Y^T \mathbf{Cx} & \mathbf Y^T \mathbf{CX} \end{pmatrix}.$$ As described above, the first column if this matrix must be zero except the first entry, which is $\sigma_1$: $$\begin{pmatrix} \mathbf y^T \mathbf{Cx} \\ \mathbf Y^T \mathbf{Cx} \end{pmatrix} = \begin{pmatrix} \sigma_1 \\ \mathbf 0 \end{pmatrix}.$$ Let’s look at the top-right entry: $\mathbf y^T \mathbf{CX}$. Since $\mathbf R_x = (\mathbf x | \mathbf X)$ is a reflector, the vector $\mathbf x$ must be orthogonal to the remaining columns, i.e., $\mathbf x^T \mathbf {X=0}$. Moreover, since $(\mathbf C^T\mathbf C – \lambda \mathbf I) \mathbf x$, it holds that $$\mathbf y^T \mathbf{CX} = \mathbf x^T \mathbf C^T \mathbf{CX} = \frac{\lambda}{\sigma_1} \mathbf x^T \mathbf X = \mathbf 0.$$ Thus,
$$\mathbf R_y\mathbf C\mathbf R_x = \begin{pmatrix} \mathbf y^T \mathbf{Cx} & \mathbf y^T \mathbf{CX} \\ \mathbf Y^T \mathbf{Cx} & \mathbf Y^T \mathbf{CX} \end{pmatrix} = \begin{pmatrix}\sigma_1 & \mathbf 0 \\ \mathbf 0 & \mathbf C_2 \end{pmatrix}$$ for some matrix $\mathbf C_2$. By the end of all this, our matrix $\mathbf A$ is decomposed as
$$\mathbf A = \mathbf U \mathbf R \mathbf V^T = \mathbf{UR}_x \begin{pmatrix}\sigma_1 & \mathbf 0 \\ \mathbf 0 & \mathbf C_2 \end{pmatrix} \mathbf R_y \mathbf V^T.$$ Critically, $\mathbf{UR}_x$ is the multiplication of two orthogonal matrices, hence orthogonal. Similarly, $\mathbf R_y \mathbf V^T$ is also orthogonal. Thus, we have not harmed the orthogonality properties that we inherited from the URV decomposition.
The remaining process is very similar — one needs to diagonalize $\mathbf C_2$, using very similar steps. Using our ingredient $$\left|\left|\begin{pmatrix}\mathbf A & 0 \\ 0 &\mathbf{B}\end{pmatrix}\right|\right| = \max\{||\mathbf A||_2, ||\mathbf{B}||_2\}$$, we’ll see that the $\sigma_2$ that emerges will have to satisfy $\sigma_1\geq \sigma_2$, which is necessary to satisfy the definition of the SVD. We will also use the last ingredient in the ingredients list, because the reflectors that we’ll create for the remaining iterations ($\mathbf P_x$, $\mathbf P_y$ etc.) will be of smaller size. Thanks to the last ingredient, the orthogonality of the URV won’t be harmed, because
$$ \mathbf{UR}_y\begin{pmatrix} \mathbf I & 0 \\ \mathbf 0 & \mathbf P_y\end{pmatrix} $$ etc. are orthogonal.